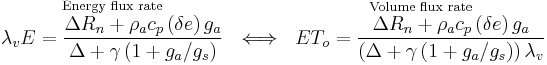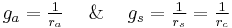Penman–Monteith equation

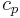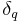Like the Penman equation, the Penman–Monteith equation (after Howard Penman and John Monteith) predicts net evapotranspiration, requiring as input daily mean temperature, wind speed, relative humidity, and solar radiation. Other than radiation, these parameter are implicit in the derivation of $\Delta$ , $c_p$ , and $\delta_q$ , if not conductances below.

The United Nations Food & Agriculture Organization (FAO) standard methods for modeling Evapotranspiration (ET) use a Penman–Monteith equation^[1]. The ASCE standard methods modify that Penman–Monteith equation for use with an hourly time step. The SWAT model is one of many GIS integrated hydrologic models^[2] estimating ET using Penman–Monteith equations.

Evapotranspiration contributions are very significant in a watershed's water balance, yet are often not emphasized in results because the precision of this component is often weak relative to more directly measured phenomena, e.g. rain and stream flow. In addition to weather uncertainties, the Penman–Monteith equation is sensitive to vegetation specific parameters, e.g. stomatal resistance or conductance^[3]. Gaps in knowledge of such are filled by educated assumptions, until more specific data accumulates.

Various forms of crop coefficients (K_c) account for differences between specific vegetation modeled and a reference evapotranspiration (RET or ET₀) standard. Stress coefficients (K_s) account for reductions in ET due to environmental stress (e.g. soil saturation reduces root zone O₂, low soil moisture induces wilt, air pollution effects, and salinity). Models of native vegetation cannot assume crop management to avoid recurring stress.

Equation

$\overset{\text{Energy flux rate}}{\lambda_v E=\frac{\Delta R_n %2B \rho_a c_p \left( \delta e \right) g_a } {\Delta %2B \gamma \left ( 1 %2B g_a / g_s \right)}} ~ \iff ~ \overset{\text{Volume flux rate}}{ET_o=\frac{\Delta R_n %2B \rho_a c_p \left( \delta e \right) g_a } { \left( \Delta %2B \gamma \left ( 1 %2B g_a / g_s \right) \right) \lambda_v }}$

λ_v = Latent heat of vaporization. Energy required per unit mass of water vaporized. (J/g)

L_v = Volumetric latent heat of vaporization. Energy required per water volume vaporized. (L_v = 2453 MJ m^-3)

E = Mass water evapotranspiration rate (g s^-1 m^-2)

ET_o = Water volume evapotranspired (m³ s^-1 m^-2)

Δ = Rate of change of saturation specific humidity with air temperature. (Pa K^-1)

R_n = Net irradiance (W m^-2), the external source of energy flux

c_p = Specific heat capacity of air (J kg^-1 K^-1)

ρ_a = dry air density (kg m^-3)

δe = vapor pressure deficit, or specific humidity (Pa)

g_a = Conductivity of air, atmospheric conductance (m s^-1)

g_s = Conductivity of stoma, surface conductance (m s^-1)

γ = Psychrometric constant (γ ≈ 66 Pa K^-1)

(Monteith, 1965)^[4]:

Note: Often resistances are used rather than conductivities.

$g_a = \tfrac{1}{ r_a} ~ ~ \And ~ ~ g_s = \tfrac{1}{ r_s} = \tfrac{1}{ r_c}$

where r_c refers to the resistance to flux from a vegetation canopy to the extent of some defined boundary layer.

Also note that 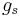$g_s$ varies over each day, and in response to conditions as plants adjust such traits as stoma openings. Being sensitive to this parameter value, the PenmanMonteith equation obviates the need for more rigorous treatment of 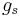$g_s$ perhaps varying within each day. Penman's equation was derived to estimate daily ET from daily averages.

A derivation of this equation may be found at http://biomet.ucdavis.edu/Evapotranspiration/PMDerivation/PMD.htm
This also explains relations used to obtain 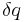$\delta q$ & $\Delta$ in addition to assumptions key to reaching this simplified equation.

Priestley–Taylor

The Priestley–Taylor was developed as a substitute to the Penman–Monteith equation to remove dependence on obsevations. For Priestley–Taylor, only radiation (irradiance) observations are required. This is done by removing the aerodynamic terms from the Penman–Monteith equation and adding an empirically-derived constant factor, $\alpha$ .

The underlying concept behind the Priestley–Taylor model is that an air mass moving above a vegetated area with abundant water would become saturated with water. In these conditions, the actual evapotranspiration would match the Penman rate of potential evapotranspiration. However, observations revealed that actual evaporation was 1.26 times greater than potential evaporation, and therefore the equation for actual evaporation was found by taking potential evapotranspiration and multiplying it by $\alpha$ . The assumption here is for vegetation with an abundant water supply (i.e. the plants have low moisture stress). Areas like arid regions with high moisture stress are estimated to have higher $\alpha$ values^[5].

References

^ Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. (1998). Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements. FAO Irrigation and drainage paper 56. Rome, Italy: Food and Agriculture Organization of the United Nations. ISBN 92-5-104219-5. http://www.fao.org/docrep/X0490E/x0490e00.HTM. Retrieved 2007-11-24.
^ Examples of GIS integrated continuous simulation hydrologic models
^ Beven, K. (1979) A sensitivity analysis of the Penman–Monteith actual evapotranspiration estimates. J. Hydrol. 44, 169–190.
^ Monteith, J.L. (1965) Evaporation and environment. Symp. Soc. Exp. Biol. 19, 205-224
Obtained from Forest Hydrology and Watershed Management – Hydrologie Forestiere et Amenagement des Bassins Hydrologiques (Proceedings of the Vancouver Symposium, August 1987, Actes du Co11oque de Vancouver, Aout 1987):IAHS-AISH Publ.no.167,1987. pp. 319–327
^ Jensen, M.E., Burman, R.D. and Allen, R.G. (1990) Evapotranspiraion and Irrigation Water Requirement. ASCE Manuals and Reports on Engineering Practices No. 70. 1st Edn., American Society of Civil Engineering (ASCE), New York, NY, USA, pp. 332–333

Jarvis, P.G. (1976) The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Phil. Trans. R. Soc. Lond. B. 273, 593–610.
Priestley, C.H.B., and Taylor, R.J. (1972) On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev., 100, 81–82.